|
|
|
| 1a. Definition of system: (colloquial) A system is a set of mutually dependent variables. | Non-systems are easier to describe than systems. Systems take much more specification. |
| 1b. Definition of system: (logically more precise) To say that a set of variables comprises a system is to hypothesize that each variable in the set is a function of every variable in the set. |
V1 = f (V1,V2,V3)
V2 = g (V1,V2,V3) V3 = h (V1,V2,V3) |
| 1c. Comment. Definition 1b. is said to be "impredicative." It is circular unless one realizes that it is meant to be used in a self-correcting inquiry process. In practice, sets of variables are said to be more or less systemically related. |
Apparent problem:
How can we know if a variable is in a system, unless we already know all the variables it interrelates with? |
| 2. Variables are sets whose elements are called values. (Endogenous variables belong to a system. Exogenous variables affect but are not part of a system.) |
V1 = {on, off}
V2 = {up, down} V3 = {day, night} |
| 3a. Dependency is a relationship among variables. To see how two (or more) variables are related, we must compute their Cartesian product, V1 x V2, which matches each value of V1 with each value of V2. We then compare observed correlations with V1 x V2 |
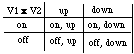
Items in the chart are correlations. |
| 3b. The more the chart is "covered" by our observations, the weaker the correlation between V1 and V2. If we observe all the value-correlations of V1 x V2 then the correlation between V1 and V2 is zero. | V1 x V2 is a display of all possible combinations of the values of V1 and V2. |
| 3c. If we observe correlate pairs from V1 x V2 such that no row and no column is repeated, we have found a one-to-one correlation. | For Chart 3a above, any two cells diagonally positioned one from the other specifies a one-to-one correlation. |
|
4a. A special relationship: functional dependency or specification.
V1 is said to be a function of V2, symbolized V1 = f (V2), if and only if any value of V1 correlates with at most one value of V2. In other words, values of V2 specify the values of V1. |
For chart 3a above, we observe (up, on), and (up, off) for light bulb variable, V1 and switch variable, V2. Are they functionally related? |
| 4b. If V1 = f (V2) and V2 = f (V1) then V1 and V2 are in one-to-one correlation. That is , each value of V1 specifies (and is specified by) one and only one value of V2. | We observe the following: (up, on, night), (up, off, day), (down, off, night) (down, off, day) Are the variables functionally related? How? |
|
5. A system is a set of variables that maintain functional relations through time, where the present state of a given variable is dependent on its own past state as well as the other variables.
An efficiently causal system (i.e. one that is precisely controllable through exogenous variables) is ultimately not time-dependent. Systems which are time-dependent are not efficiently-causal. |
V1 at t+1 = f (V1 at t, V2 at t), where t is a point in time and t+1 the next identified point in time.
(Pace, Mathematicians! For practical purposes we are working with instrumentally measured, i.e. rational, not real, numbers. The "next point in time" is the next interval specified by some kind of clock.) |