|
|
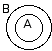
|
|
|
|
|
|
|
|
|
|
I.
Showing Logical Relations with Venn* Diagrams
©1999 Edward G. Rozycki
The relationships between two classes (categories) of things can be consistently and powerfully visualized using Venn diagrams. In this workbook we will be interested in showing the relationships between pairs and triples of categories. This will require your becoming familiar with the way they can combine.
The Basic Relations show how the relationships between two classes of objects can be represented. What is important about these drawings is how their boundaries exclude, include or overlap one another. Although the use of circles is traditional, it is not necessary. Ovals or rectangles may be sometimes be used. Also, the relative size of the figures has no meaning. A big circle does not necessarily have more items in it than a small one.
|
|
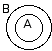
|
|
|
|
|
|
|
|
|
|
Imagine the circles as boundaries containing all items of the class it names. So in figure 1 we see that if we arbitrarily let A = the class of all felines and B = the class of all cars, nothing in A can also be in B, and vice versa. (We could have as easily let A = the class of all cars and B = the class of all felines. It would not matter for this relationship.) This is because their boundaries do not overlap. Nothing that is a feline is also a car and vice-versa.
In figure 2, it is not arbitrary which class circles A and B symbolize. We only get a diagram of a true relationship if we assign B = all cars and A = all TransAms. Then because every example of a TransAm is also a car, the boundary of A is contained entirely within the boundary of B. However, because not every car is a TransAm, the boundary of B contains space not within the boundary of A.
In figure 3 we see an overlap between A and B. It is arbitrary in this case which figure we use to indicate the class of all felines and the class of all things Asian. Let's let A= class of all felines and B = class of all things Asian. Clearly there are some felines that are not Asian, there are Asian felines and there are Asian things that are not feline. The diagram illustrates this nicely.
There are eleven different possible combinations of relationships among three classes. For each of the diagrams below, three applicable classes are given. Identify which is class A, B, and C. Some choices may be arbitrary. (Note that simple descriptions such as "aquatic" or "dangerous" are short expressions for "things that are aquatic" or "things that are dangerous.")
|
|
|
|
|
I. |
cattle books |
A=
B= C= |
|
II. |
books TransAms |
A=
B= C= |
|
III. |
mammals reptiles |
A=
B= C= |
|
IV. |
aquatic Hondas |
A=
B= C= |
V. 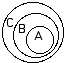
|
cars vehicles |
A=
B= C= |
VI. 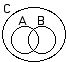
|
warm-blooded vertebrate |
A=
B= C= |
VII. 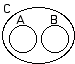
|
cows sharks |
A=
B= C= |
|
VIII. |
fish terrestrial |
A=
B= C= |
IX. 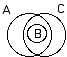
|
terrestrial animals |
A=
B= C= |
X. 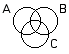
|
warm-blooded aquatic |
A=
B= C= |
XI. 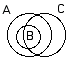
|
birds carnivorous |
A=
B= C= |
*What we have been calling "Venn" diagrams, following mistaken tradition, are actually "Euler" diagrams. Pace matematica!
Now that you have seen examples of how three classes can relate to one another, test your ability to recognize which relationship exhibited in one of the eleven diagrams below matches with a set of categories from the third column.
First, within each group choose which matching set goes with each diagram. Second, use that matching set to fill in the class identifications next to each diagram.
Group A
|
|
|
|
|
I. |
A=
B= C= |
1. birds
aquatic rodents |
|
II. |
A=
B= C= |
2. music
cattle weapons |
|
III. |
A=
B= C= |
3. metal
tools evergreens |
|
IV. |
A=
B= C= |
4.mammals
canines Buicks |
Group B
|
|
|
|
V. 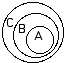
|
A=
B= C= |
5. animals
rabbits aquatic |
VI. 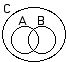
|
A=
B= C= |
6. birds
owls storks |
VII. 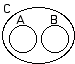
|
A=
B= C= |
7. animals
horned cattle |
|
VIII. |
A=
B= C= |
8. beverages
sodas ginger ales |
Group C
|
|
|
|
|
VIII. |
A=
B= C= |
8. metal
useful expensive |
IX. 
|
A=
B= C= |
9. whales
aquatic animals |
X. 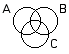
|
A=
B= C= |
10. animals
reptiles herbivorous |
XI. 
|
A=
B= C= |
11. animals
aquatic rabbits |
V. Judging Truth or Falsity From Venn Diagrams
To test your understanding of the way Venn diagrams represent the relationships among classes of objects, pick the sentences from the three offered that are true in terms of the diagram and the values given for A, B and C. The sentence may be factually false when judged against outside information.
|
|
|
|
1. 
|
A=pianos
B=spinets C=Yamahas |
1. All pianos are spinets.
2. Some Yamahas are pianos. 3.All spinets are Yamahas. |
2. 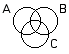
|
A=radios
B=SONY C=functioning |
1. All radios are SONYs.
2. No radios are functioning. 3.Some functioning radios are SONYs.. |
3. 
|
A=widgets
B=gadgets C=brizzles |
1. All gadgets are brizzles.
2. All widgets are brizzles. 3. No brizzles are widgets. |
|
4. |
A=meat
B=hamburgers C=edible |
1. Meat is never edible.
2. All meat is edible. 3.No hamburgers are edible. |
5. 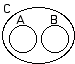
|
A= candy bars
B=eclairs C= fattening |
1. Some eclairs are not fattening.
2. No candy bars are fattening. 3.No candy bars are eclairs. |
6. 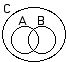
|
A= monkeys
B= intelligent C= poker players |
1. Some stupid monkeys play poker.
2. All poker players are intelligent. 3. No intelligent people play poker. |
7. 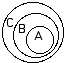
|
A= Martians
B= space travellers C= humanoid |
1. All humanoids are space travellers.
2. All Martians are humanoid. 3. No space travellers are humanoid. |
|
8. |
A=evil-doers
B= convicts C= Muppets |
1. No evil-doers are Muppets..
2. Some convicts are Muppets. 3.All convicts are evil-doers. |
|
9. |
A=French speakers
B= Italian speakers C= Dutch speakers |
1. Some people speak three languages.
2. No French speaker speaks Dutch.. 3.All Dutch speakers speak Italian. |
|
10. |
A= students
B= teachers C= gamblers |
1. No gamblers are teachers.
2. All students are teachers. 3. Some gamblers are students.. |
|
11. |
A=pickles
B= perfume C= gifts |
1. Some gifts are perfume.
2. Some pickles are perfume. 3. No pickles are gifts. |